Y = x 2 5x 3; The graph has the same shape as y = x^2, but there are some shifts Replacing x with x2 makes x=2 act in the new equation just like x=0 did in the old one (That is where I would find 0^2) That shifts the graph 2 to the right Compare y = x^2 and y3 = (x2)^2 Replacing x with x2 moves the graph 2 in the positive x direction (2 to the right)Parabola Calculator This calculator will find either the equation of the parabola from the given parameters or the axis of symmetry, eccentricity, latus rectum, length of the latus rectum, focus, vertex, directrix, focal parameter, xintercepts, yintercepts of the entered parabola To graph a parabola, visit the parabola grapher (choose the
From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4
Y=(x+4)^2-2 parabola
Y=(x+4)^2-2 parabola- Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downWhat is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form, use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$ Answer the axis of symmetry is the line $$ x = 1 $$ Problem 7 What is the following parabola



How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube
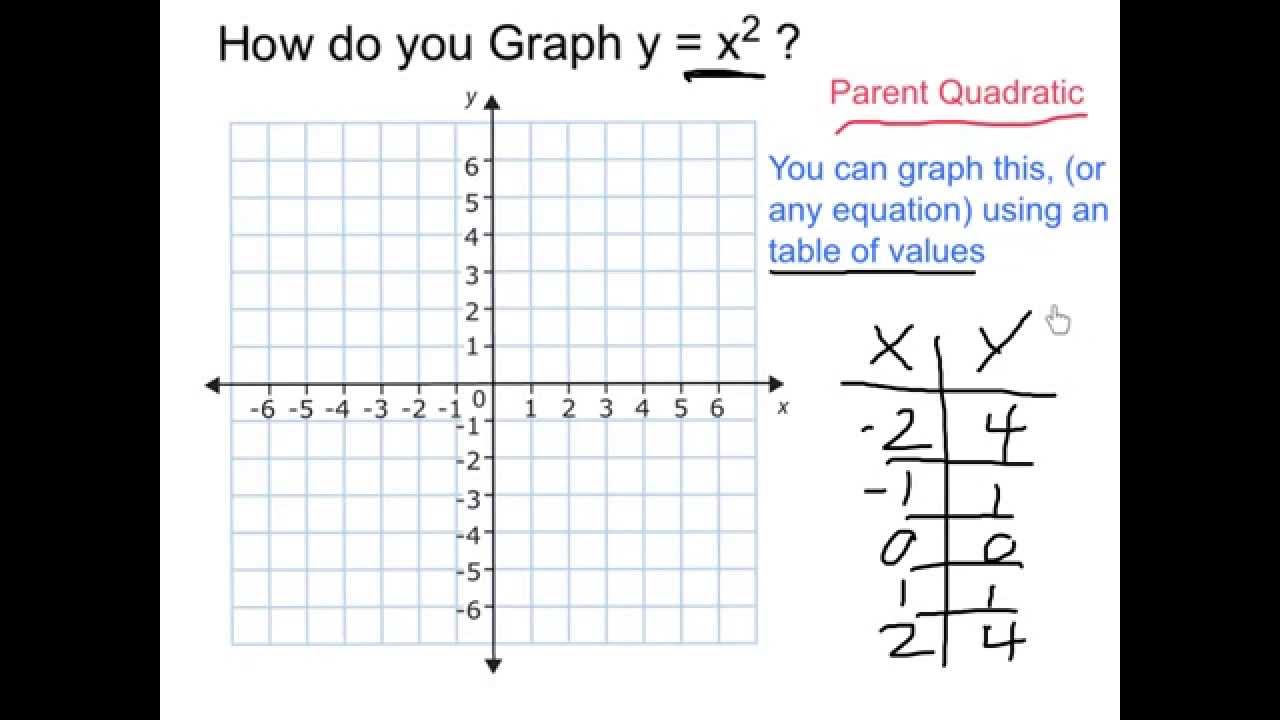
We're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Thanks for contributing an answer to Mathematics Stack Exchange!I do not know how to graph the parabola y= x^2 Plot a few points and draw a smooth curve thru them
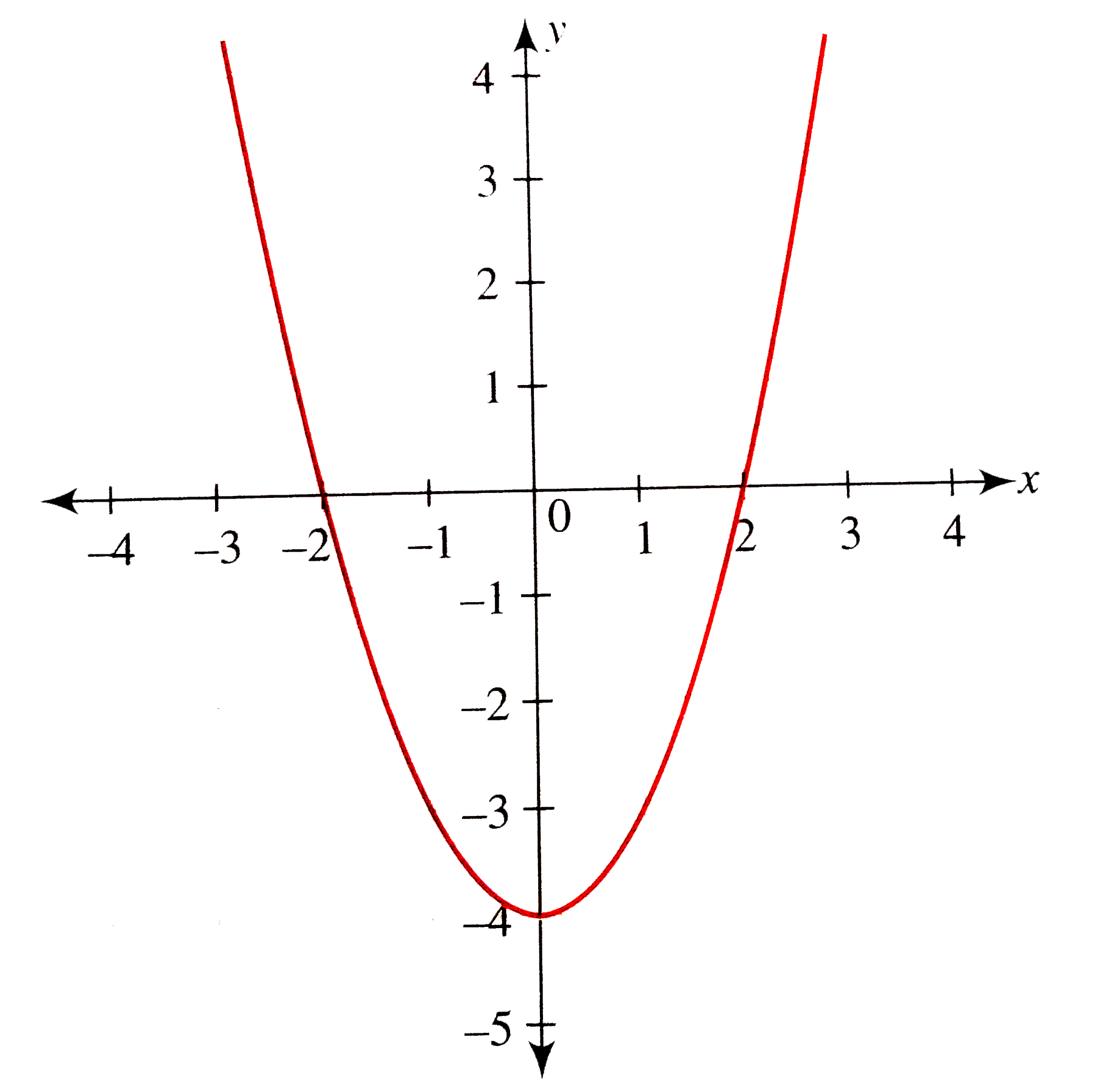
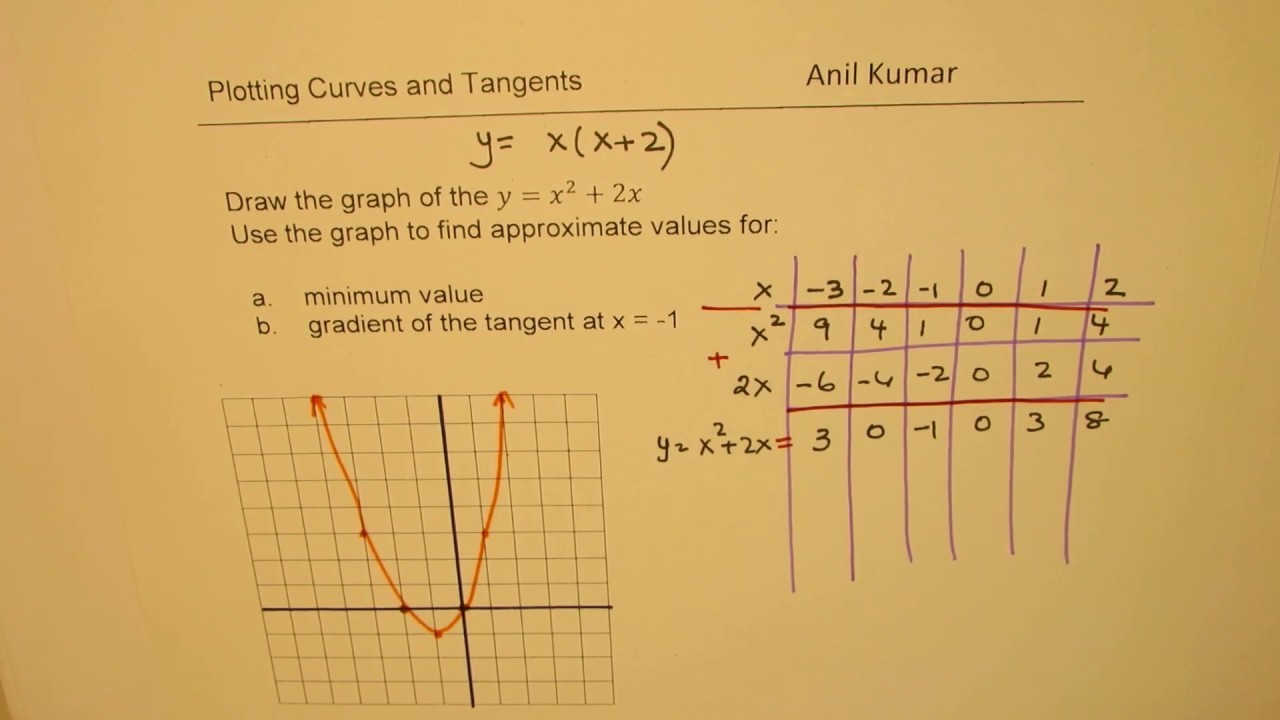
The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetryY = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is y = x 2, where x ≠ 0 Here are a few quadratic functions y = x 2 5;
Sideways Parabolas 1 Cool Math has free online cool math lessons, cool math games and fun math activities Really clear math lessons (prealgebra, algebra, precalculus), cool math games, online graphing calculators, geometry art, fractals, polyhedra, parents and teachers areas tooHere is the graph of the parabola y=x² Here is the graph of the line y=x2 Now we'll find the coordinates of those two points where they intersect Substitute for y in the second equation Get 0 on the right Factor the left side Use the zero factor principle x2 = 0 x1 = 0 x = 2 x = 1 Now we have to find the y coordinates to go with eachIn the figure, the vertex of the graph of y=x 2 is (0,0) and the line of symmetry is x = 0 Definition Parabola 1Algebric A Parabola is the graph of a quadratic relation of either form where a ≠ 0;




From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4



How To Graph A Parabola Y X 5 2 3 Socratic
Mathy=x^2bxc/math What we are really looking for is a value for mathb/math and mathc/math Once we can find those two values, we can simply plug them back into mathy=x^2bxc/math to get the equation of the parabola Let's start The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equation rosieweber04 rosieweber04 Mathematics High School answered The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equation 2 See answersBut avoid Asking for help, clarification, or responding to other answers



Solution Graph The Parabola Y X 4 2 2




Vertical Shifts Of Quadratic Functions Ck 12 Foundation
Y = 02x 2 04x 28 Those two parabolas look this way Now, where the two parabolas cross is called their points of intersection Certainly these points have (x, y) coordinates, and at the points of intersection both parabolas share the same (x, y) coordinates So, at the points of intersection the (x, y) coordinates for f(x) equal the (x This should do import matplotlibpyplot as plt import numpy as np # create 1000 equally spaced points between 10 and 10 x = nplinspace (10, 10, 1000) # calculate the y value for each element of the x vector y = x**2 2*x 2 fig, ax = pltsubplots () axplot (x, y) This is your approach with as few changes as possible to make it workA particle moves along the parabola {eq}y = x^2 {/eq} in the first quadrant in such a way that its {eq}x {/eq}coordinate (measured in meters) increases at a steady {eq}\rm 10\ m/sec {/eq} How



Instructional Unit The Parabola Day 4 And 5




Consider The Parabola Y X 2 The Shaded Area Is Brainly In
Graphing Basic Parabola Y X 2 Youtube For more information and source, see on this link https//myoutubecom/watch?v=qgFZ6SBs6UcY = x 2 3x 13;Please be sure to answer the questionProvide details and share your research!




Content Transformations Of The Parabola




Plot A Graph For The Equation Y X 2 4x 1
The equation of the common tangent touching the circle (x – 3)^2 y^2 = 9 and the parabola y^2 = 4x is asked in Coordinate geometry by AmreshRoy (The Parabola Given a quadratic function \(f(x) = ax^2bxc\), it is described by its curve \y = ax^2bxc\ This type of curve is known as a parabolaA typical parabola is shown here Parabola, with equation \(y=x^24x5\)Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis



Draw The Graph Of Y X 2 3x 2 And Use It To Solve X 2 2x 1 0 Sarthaks Econnect Largest Online Education Community



Quadratics Graphing Parabolas Sparknotes
Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and yExample 3) Graph y = x 2 4x 7 a = 1, b = 4, and c = 7 Since a 0 the parabola opens up (is U shaped) To find the x intercept we plug in 0 for y 0 = x 2 4x 7 (this expression does not factor so we have to use the quadratic formula) Since the roots are imaginary the parabola has no xintercepts We find the yintercepts by plugging math Consider a parabola P that is congruent (has the same shape) to y=x^2 , opens upward, and has vertex (2,3) Now find the equation of a new parabola that results if P is Compressed to a factor of 1/2 Translated 2 units to the left Translated 3 units up Reflected in the xaxis and translated 2 units to the right and 4 units down



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



Graphing Quadratic Functions
The simplest parabola is y = x 2 but if we give x a coefficient, we can generate an infinite number of parabolas with different "widths" depending on the value of the coefficient ɑ So lets make y = ɑx 2 In the graph below, ɑ has various values Notice that when ɑ is negative, the parabola is "upside down"Question I do not know how to graph the parabola y= x^2 Found 2 solutions by stanbon, jim_thompson5910 Answer by stanbon(757) (Show Source) You can put this solution on YOUR website!Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience




How To Graph A Parabola With No X Intercepts Y X 2 2 Youtube



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
Graphing Basic Parabola Y X 2 Youtube For more information and source, see on this link https//myoutubecom/watch?v=qgFZ6SBs6Uc Notice that the column E contains values for #color(red)(x^2# #y=x^2# is the Parent Function for a quadratic equation The graph of #y=x^2# is useful in understanding the behavior of the function given #color(red)(y = 4x^2# Since, the sign of the #x^2# term is positive, the parabola opens up and we have a Minimum point at the Vertex #colorDirection Opens Down Vertex (5 2, 17 4) ( 5 2, 17 4) Focus (5 2,4) ( 5 2, 4) Axis of Symmetry x = 5 2 x = 5 2 Directrix y = 9 2 y = 9 2 Select a few x x values, and plug them into the equation to find the corresponding y y values The x x values should be selected around the vertex



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




Parabola Parent Function Mathbitsnotebook A1 Ccss Math
Set y y equal to the new right side y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down The first thing I recognize in that equation is the y 2 term, which tells me it will be a parabola (It won't be a circle, ellipse or hyperbola because there is an x term, but no x 2 term See Conic Sections) Let's start with the most basic parabola y = x 2 and build up to the required answer Example 1 y = x 2 To solve x 2 3x – 4 = 0 subtract x 2 3x – 4 = 0 from y = x 2 3x – 4, The points of intersection of the parabola with the x axis are the points (4, 0) and (1, 0), whose x – coordinates (4, 1) is the solution, set for the equation x 2 3x – 4 = 0



Practice Exam 1



Graph Y X 2 Youtube
The equation of the common tangent touching the circle (x − 3) 2 y 2 = 9 and the parabola y 2 = 4 x above the xaxis is View solution Two straight lines are perpendicular to each other, one of them touches the parabola y 2 = 4 a ( x a ) and the other touches y 2 = 4 b ( x b )The graph of y= (xk)²h is the resulting of shifting (or translating) the graph of y=x², k units to the right and h units up For example, y= (x3)²4 is the result of shifting y=x² 3 units to the right and 4 units up, which is the same as 4 units down This is the currently selected itemNo calculus required for this (or really any tangent to algebraic curve problem) We zoom into our parabola near mathx=1/math mathy = x^2 = ( 1 (x 1
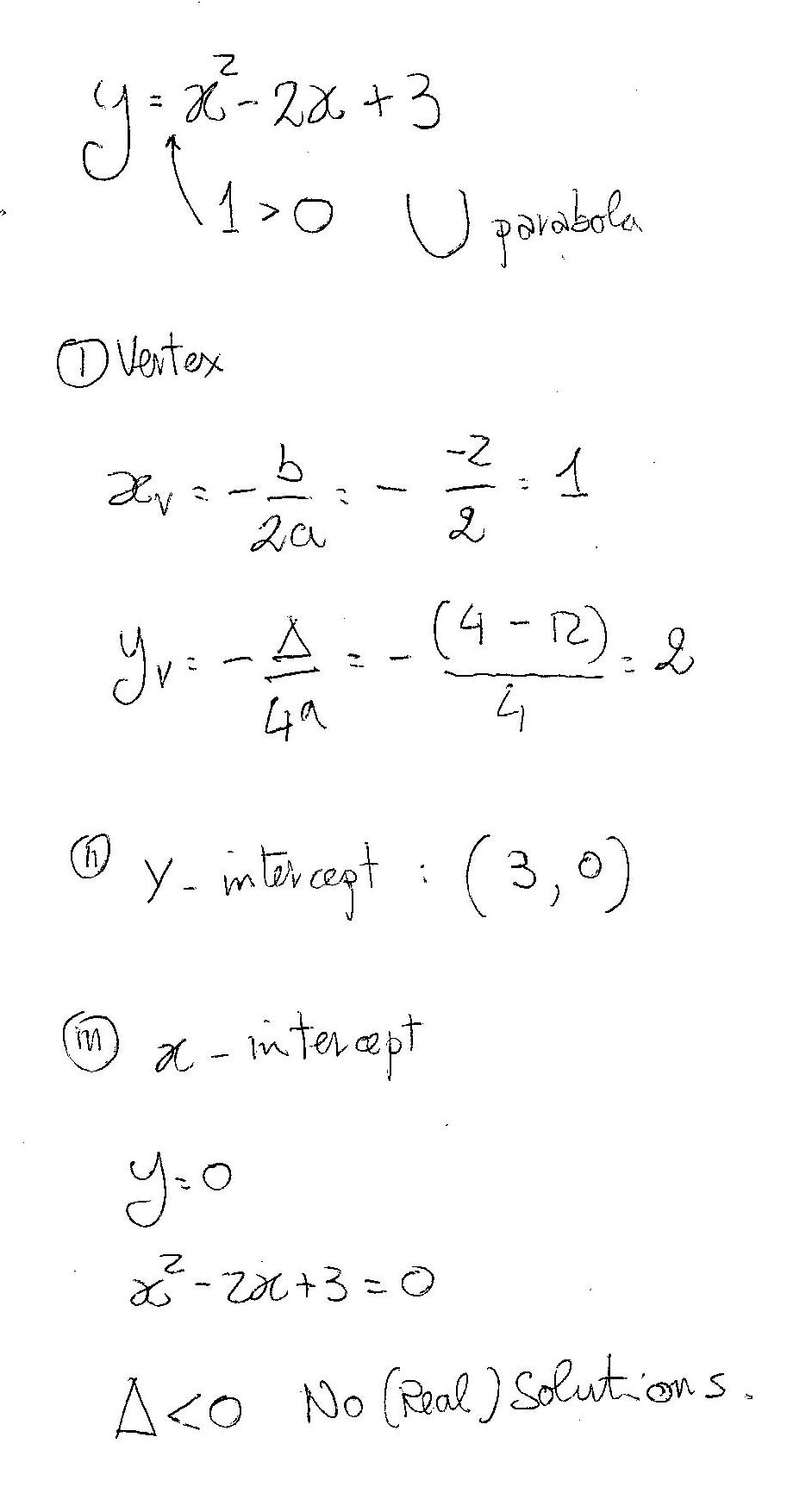



How Do You Graph Y X 2 2x 3 Socratic




How To Draw Y 2 X 2
When graphing parabolas, find the vertex and yinterceptIf the xintercepts exist, find those as wellAlso, be sure to find ordered pair solutions on either side of the line of symmetry, x = − b 2 a Use the leading coefficient, a, to determine if aThe parabola y=x2 2y=x 2 y, equals, x, start superscript, 2, end superscript is reflected across the xxxaxis and then scaled vertically by a factor of 4/3 3 4 start fraction, 4, divided by, 3, end fraction Reply to bhbond's post "The parabola y=x2 2y=x 2Parabolas A quadratic function is a function that can be written in the form f ( x) = a x 2 b x c where a, b, and c are real numbers and a ≠ 0 This form is called the standard form of a quadratic function The graph of the quadratic function is a Ushaped curve is called a parabola The graph of the equation y = x 2, shown below, is a



Exploration Of Parabolas




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
You have conic y = x 2, so matrix M is given by π 4 0 0 0 1) x 2 − 2 x y y 2 − x 2 − y 2 = 0 Your result is corect This is the plot in geogebraorg where t ∈ R You are rotating each point of the parabola, and hence X ( t) Y ( t) = 2 2 1 − 1 1 1 ⋅ x ( t) y ( t) = 2 2 439 answers 716K people helped You don't say what the goal of this problem is, which leaves others guessing I'd venture that you want to know how the function y=x^2 changes if the graph (parabola) is shifted up by 4 units This is vertical translation The new function will be g (x) = x^2 4 kvargli6h and 41 more users found this answerKey Takeaways The graph of any quadratic equation y = a x 2 b x c, where a, b, and c are real numbers and a ≠ 0, is called a parabola;
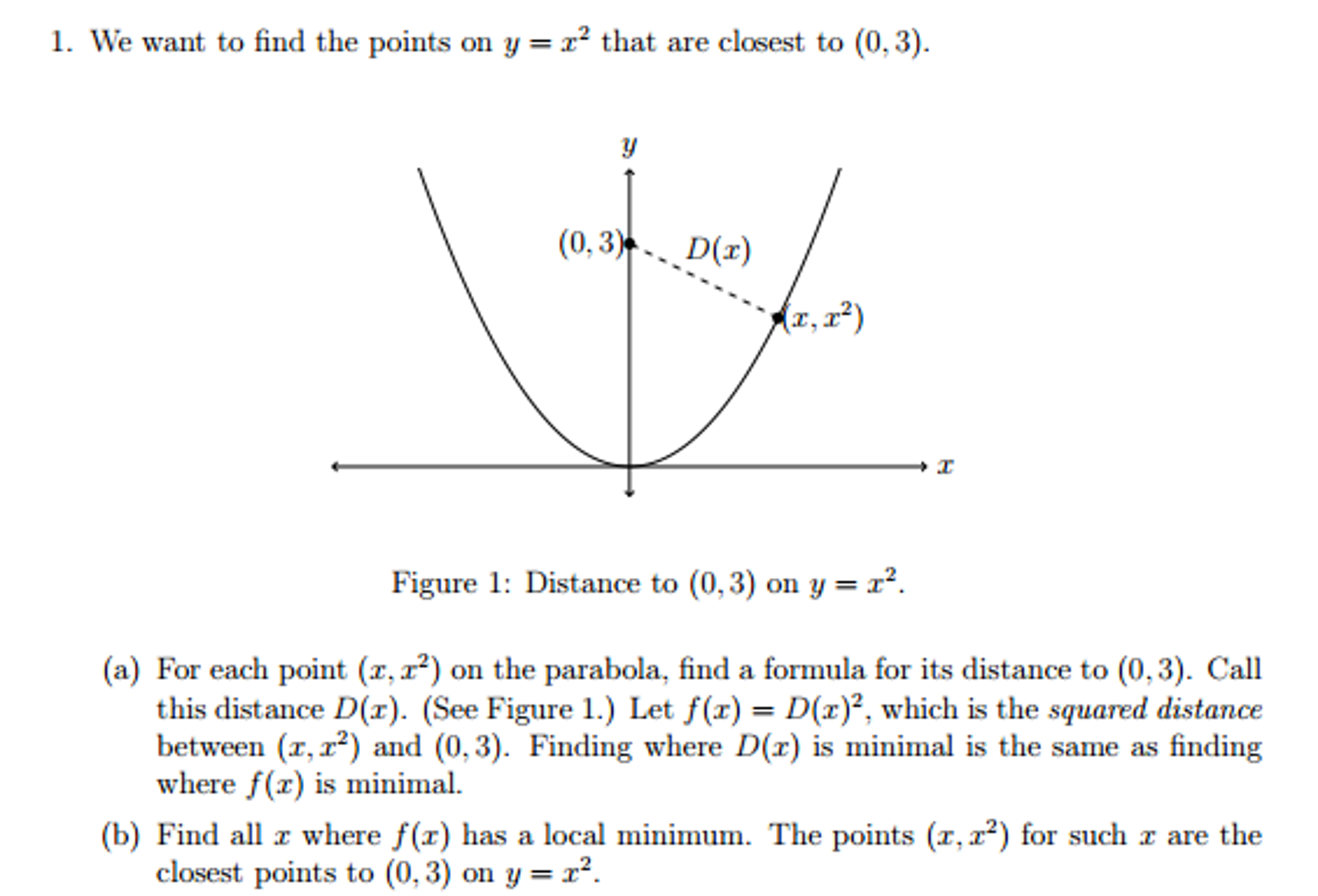



We Want To Find The Points On Y X 2 That Are Chegg Com



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic
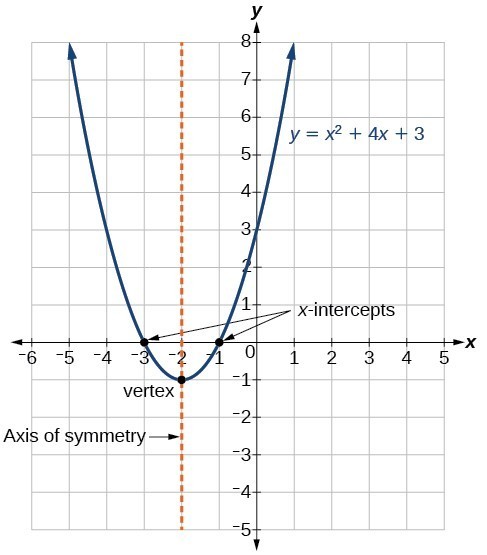
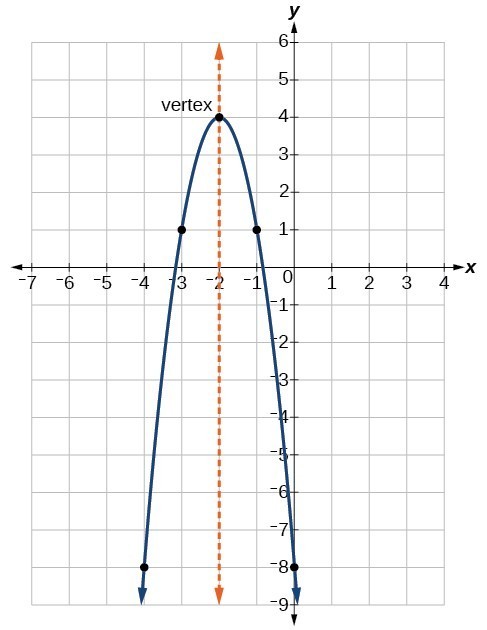
The x coordinate of the vertex is the equation of the axis of symmetry of the parabola The vertex of the parabola is ( 2, 1) So, the axis of symmetry is the line x = 2 Find the axis of symmetry of the graph of y = x 2 − 6 x 5 using the formula For a quadratic function in standard form, y = a x 2 b x c , the axis of symmetry is aThe vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3) Observe the graph of yExploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts




Quadratic Function



The Parabola Y X 2 C Is To Be Tangent To The Line X Y What Is The Value Of C Quora
The children are transformations of the parent Some functions will shift upward or downward, open wider or more narrow, boldly rotate 180 degrees, or a combination of the above Learn why a parabola opens wider, opens more narrow, orStep 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} StepConsider the parabola y = x^2 The shaded area is 12th Maths Application of Integrals Area Under Simple Curves Consider the parabola y = x




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic



Graphing Quadratic Functions



1




How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube



How To Graph A Parabola Y X 5 2 3 Socratic




Graph Y X 2 3 Youtube



Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3




How To Draw Y 2 X 2
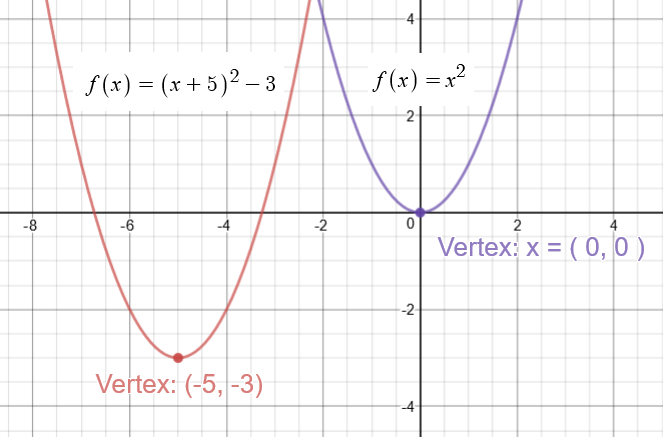



How To Graph A Parabola Y X 5 2 3 Socratic




Quadratic Function



Quadratics Graphing Parabolas Sparknotes



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2




Content Transformations Of The Parabola
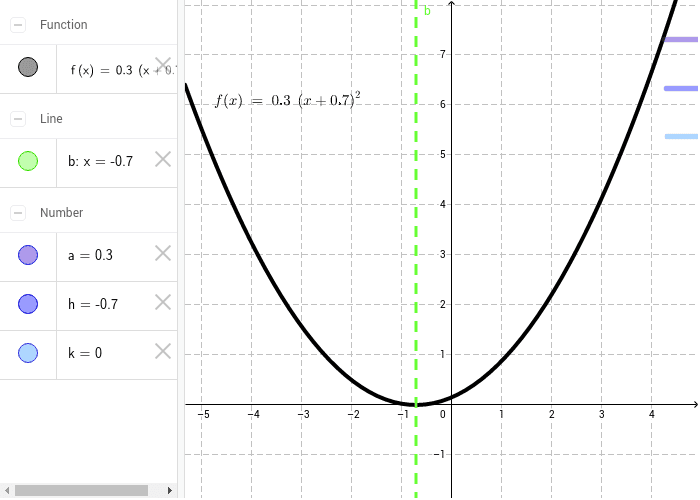



Transformations To The Graph Of Y X 2 Geogebra



The Line Y 2x 9 Is Tangent To The Parabola Y X 2 Ax B At The Point 4 1 What Are The Values Of A And B Quora




How To Draw Y 2 X 2
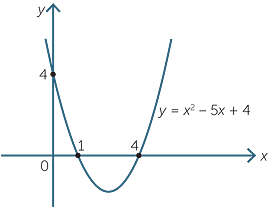



Quadratic Function
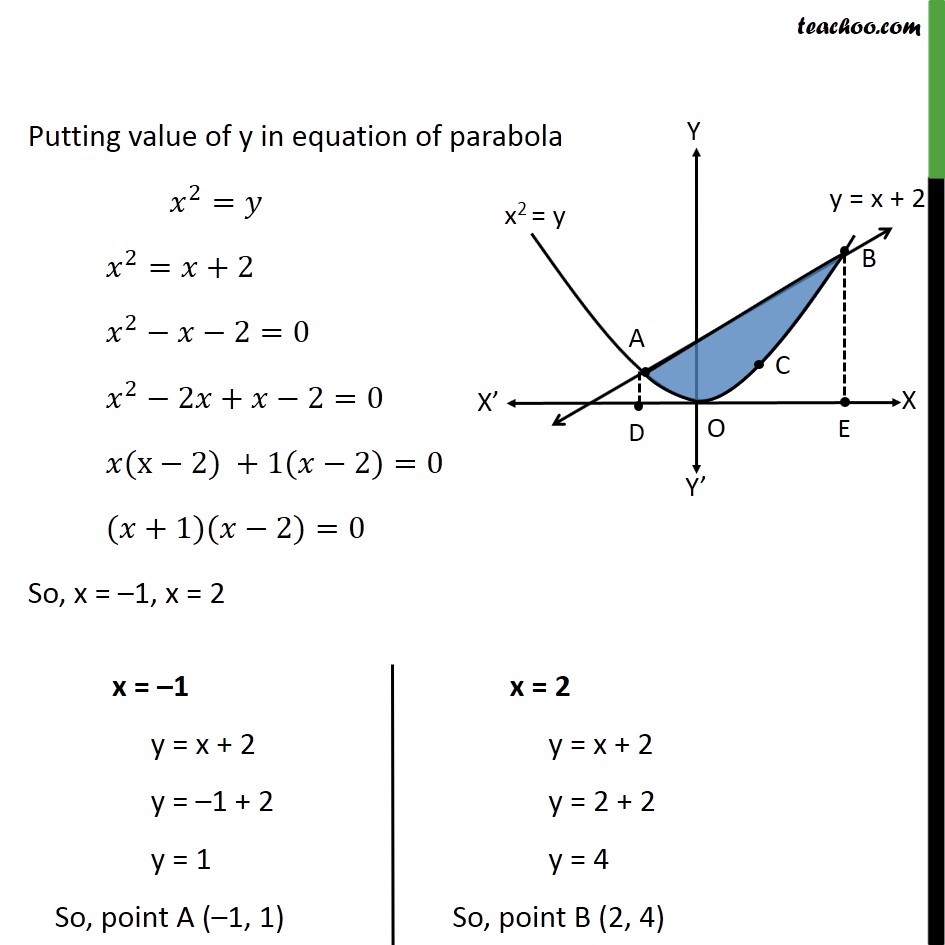



Misc 10 Find Area Enclosed By Parabola X2 Y T X 2



Search Q Y 3d1 X Tbm Isch



Math Spoken Here Classes Quadratic Equations 3
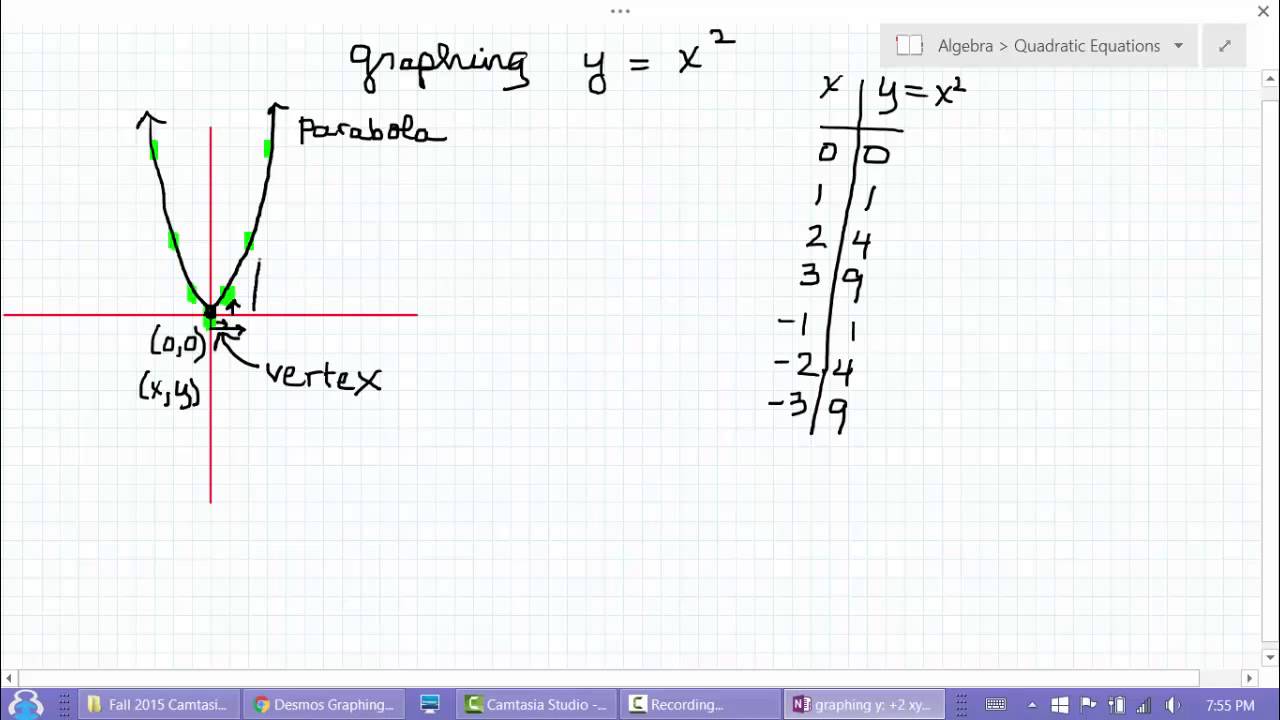



Graphing Simple Non Linear Relationships 9 Alamandamaths




Content Transformations Of The Parabola




Three Tangent Lines To The Parabola Y X 2 Corresponding To Three 1d Download Scientific Diagram




How Do You Graph Y X 2 1 Socratic



Quadratics Graphing Parabolas Sparknotes




How Do You Graph Y X 2 2x Socratic




Find The Area Of The Region Bounded By The Parabola Y 2 2x 1 And The Line X Y 1
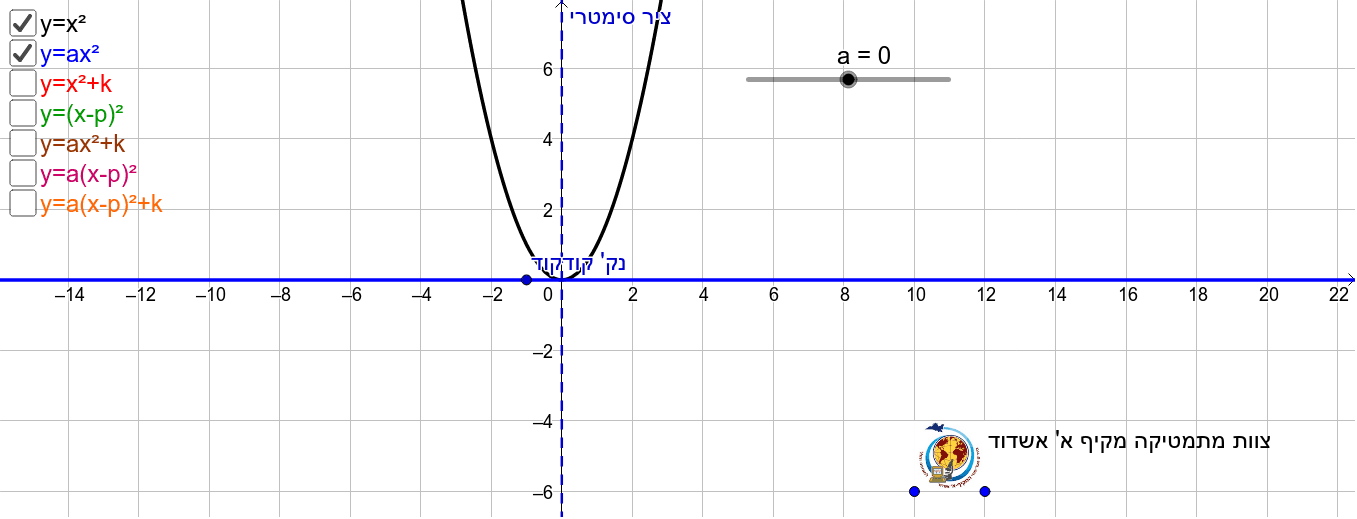



Parabola Y X 2 Geogebra




The Graph Of The Quadratic Function Y X2 Is Shown Below If This Parabola Is Reflected About The Brainly Com




Find The Axis Of Symmetry 1 And The Vertex 2 Of A Parabola Ppt Download



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively



Solution I Do Not Know How To Graph The Parabola Y X 2
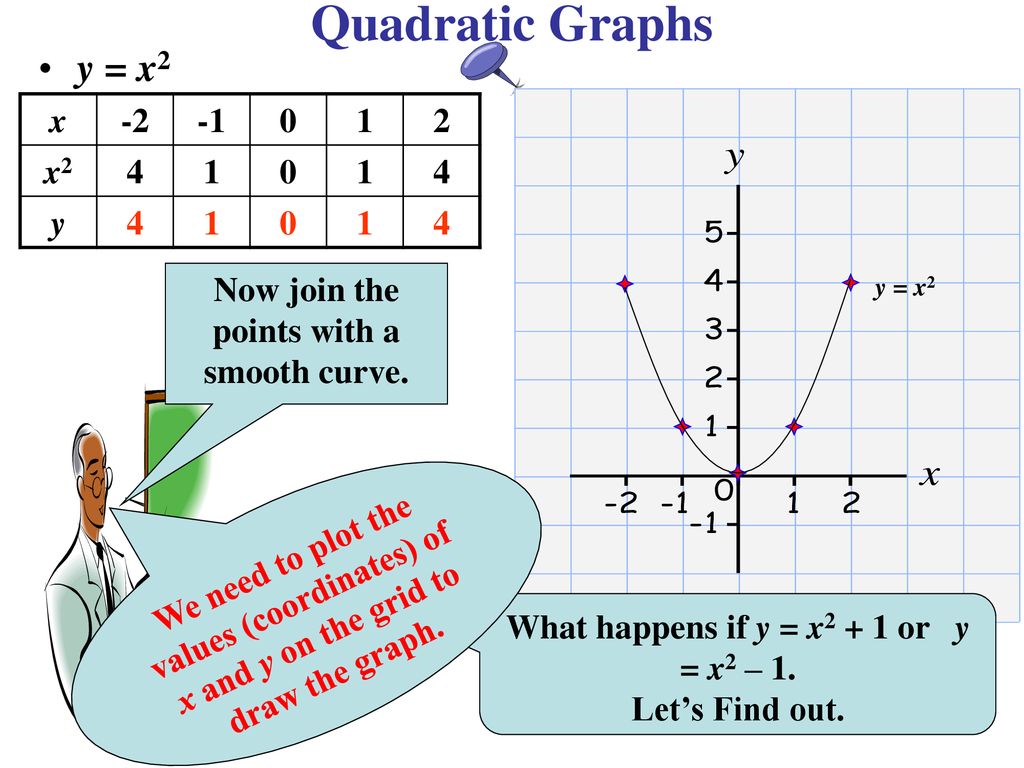



Quadratic Graphs Parabolas Ppt Download
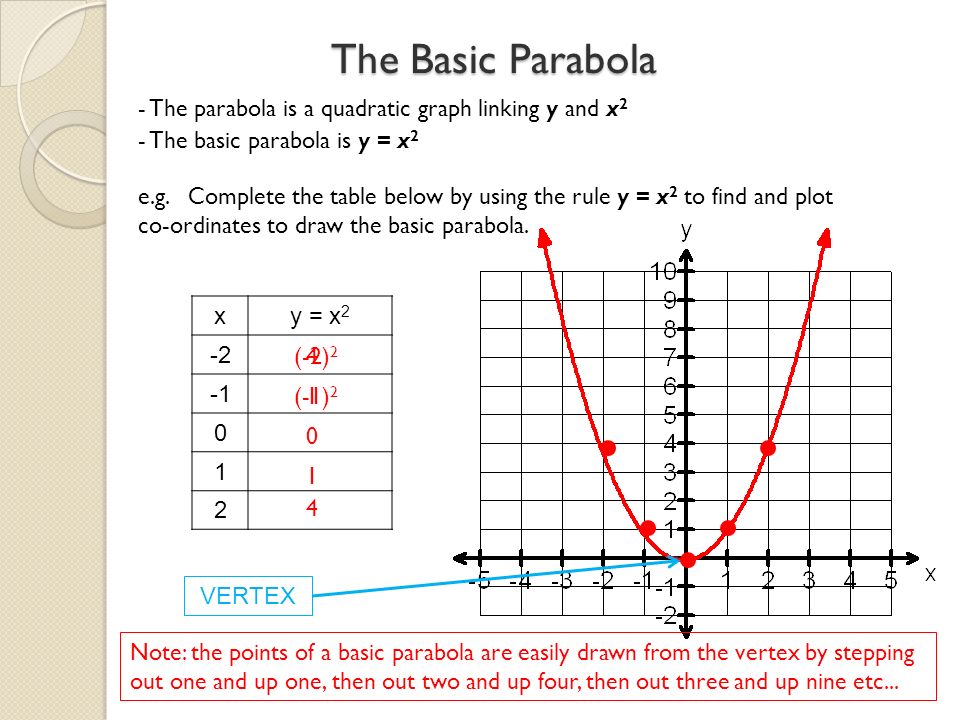



Parabolas Ppt Download




Graph Y X 2 Study Com
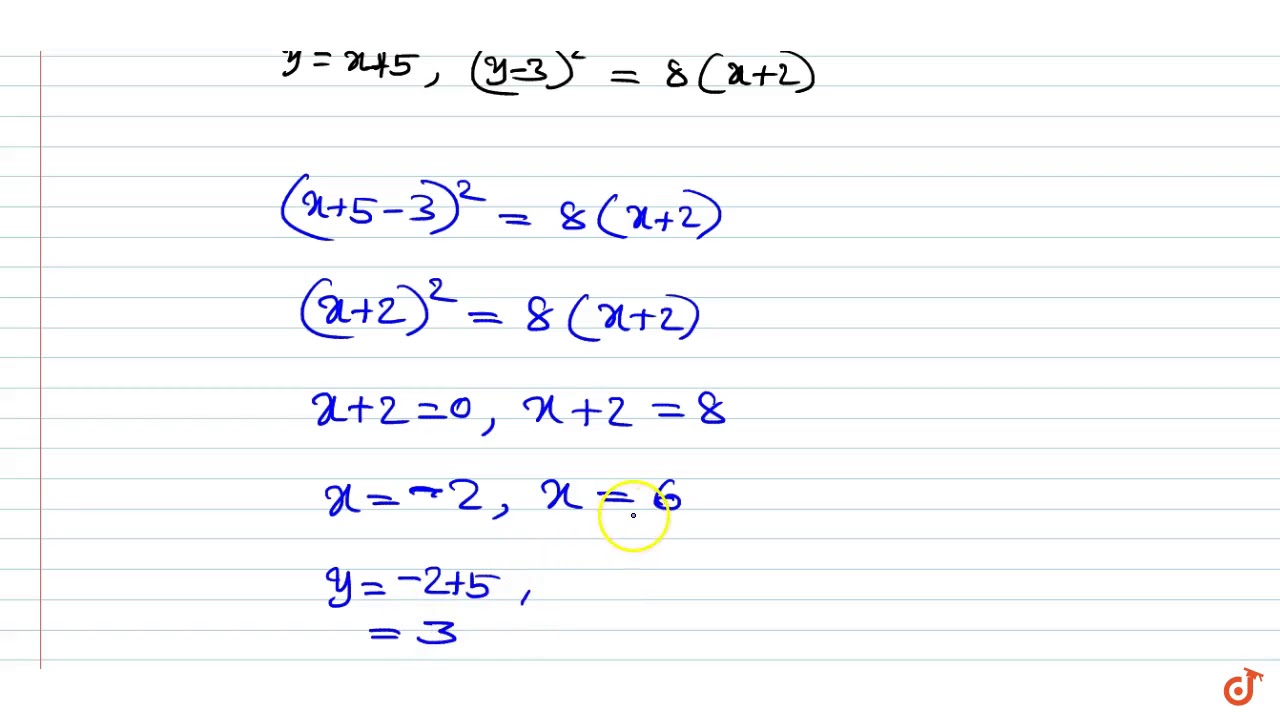



A Line Y X 5 Intersect The Parabola Y 3 2 8 X 2 At A B Find The Length Of Chord Ab Youtube




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0




Quadratic Function




Vertex Of A Parabola Iitutor




The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Li
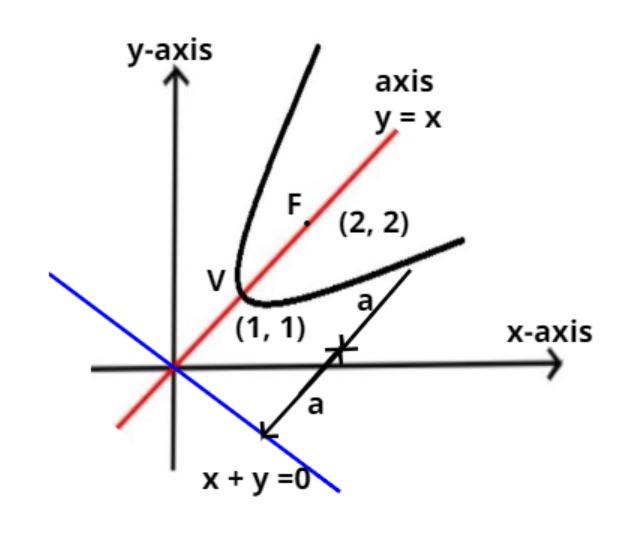



The Axis Of A Parabola Is Yx And The Vertex And The Class 11 Maths Cbse



Parabolas



Graphing Quadratic Functions




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
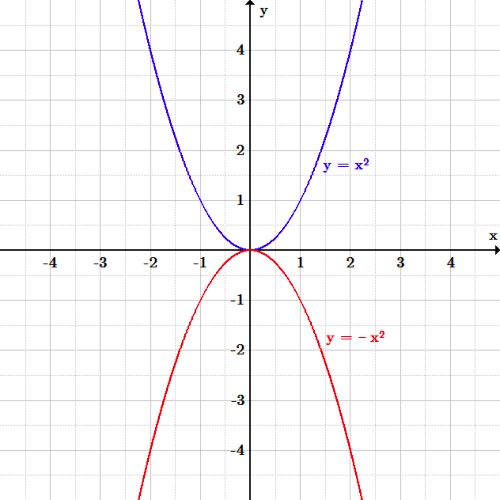



Transformations Boundless Algebra
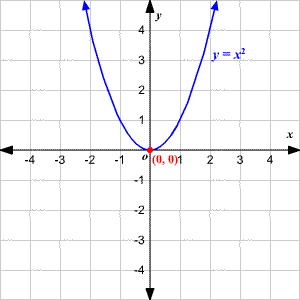



Parabolas



Math Spoken Here Classes Quadratic Equations 3



1




Example 15 Find Area X Y 0 Y X2 1 0 Y X 1



Math Spoken Here Classes Quadratic Equations 3




Y X 2
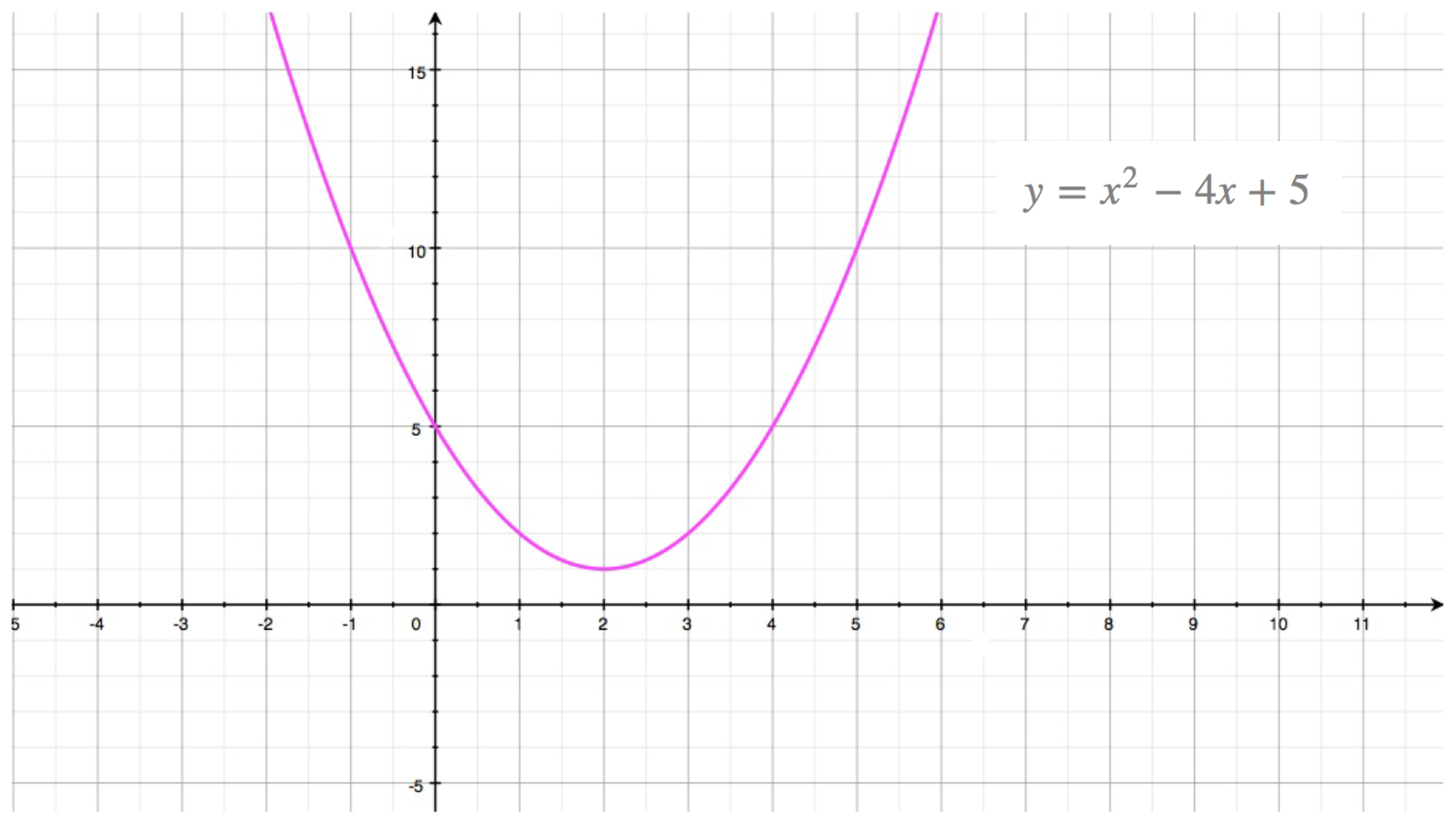



Quadratic Function Parabola
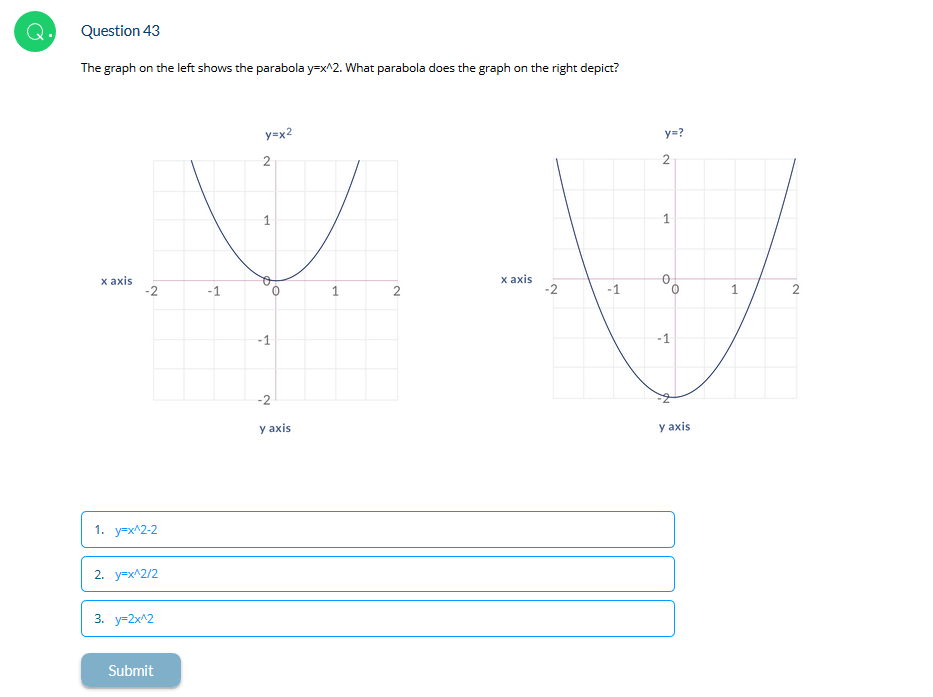



Question 43 The Graph On The Left Shows The Parabola Chegg Com




Image Of A Parabola Whose Equation In The Object Plane Is Y X 2 And Image Of Parabola Whose Equation Is Y 1 X 2 Mathematics Stack Exchange
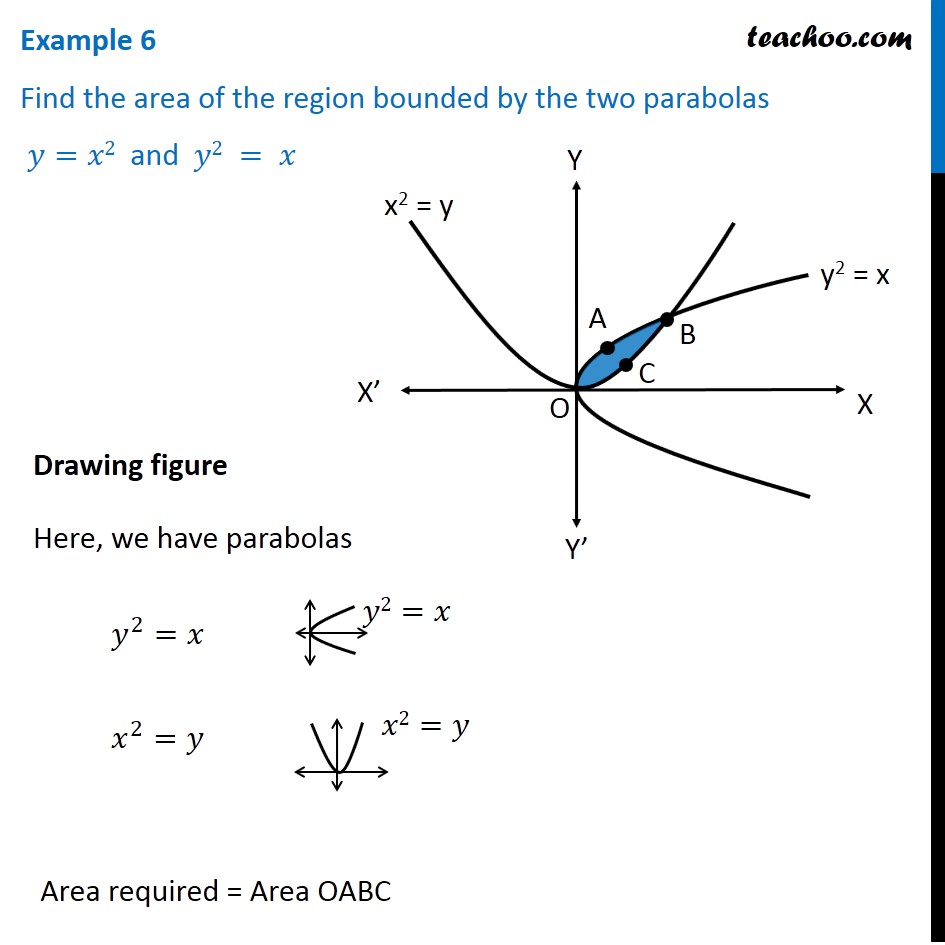



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X




Graphing Quadratic Functions Lesson Article Khan Academy




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com



Graphing Quadratic Functions



Find The Area Of The Region Enclosed By The Parabola X2 Y And The Line Y X 2 Studyrankersonline




Topology Types Of The Offsets To The Parabola Y X 2 Download Scientific Diagram



Y X 2



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
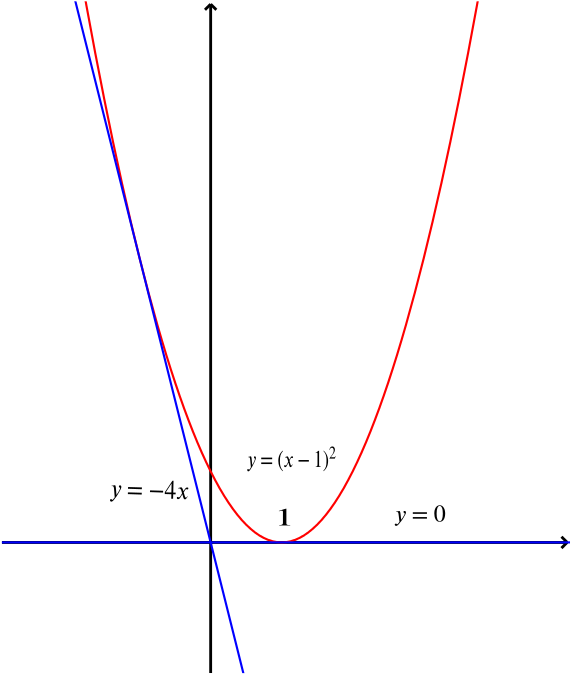



Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics




Consider The Parabola Whose Equation Is Y X 2 4x And The L




Scaling Reflecting Parabolas Video Khan Academy
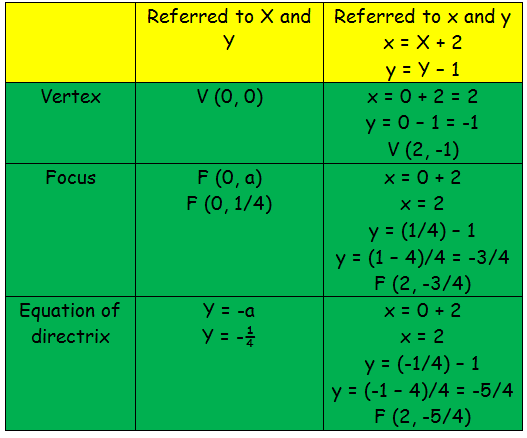



How To Find Focus Directrix And Vertex Of Parabola




The Line Y X 2 Cuts The Parabola Y 2 8x In The Points A And B The Normals Drawn To Youtube



How To Draw A Sketch Of The Graph Of The Parabola Y X 2 8x 10 Quora




The Distance Between The Vertex Of The Parabola Y X 2 4x



Quadratics Graphing Parabolas Sparknotes



Solution How To Graph A Parabola Using Y X2 2x 8
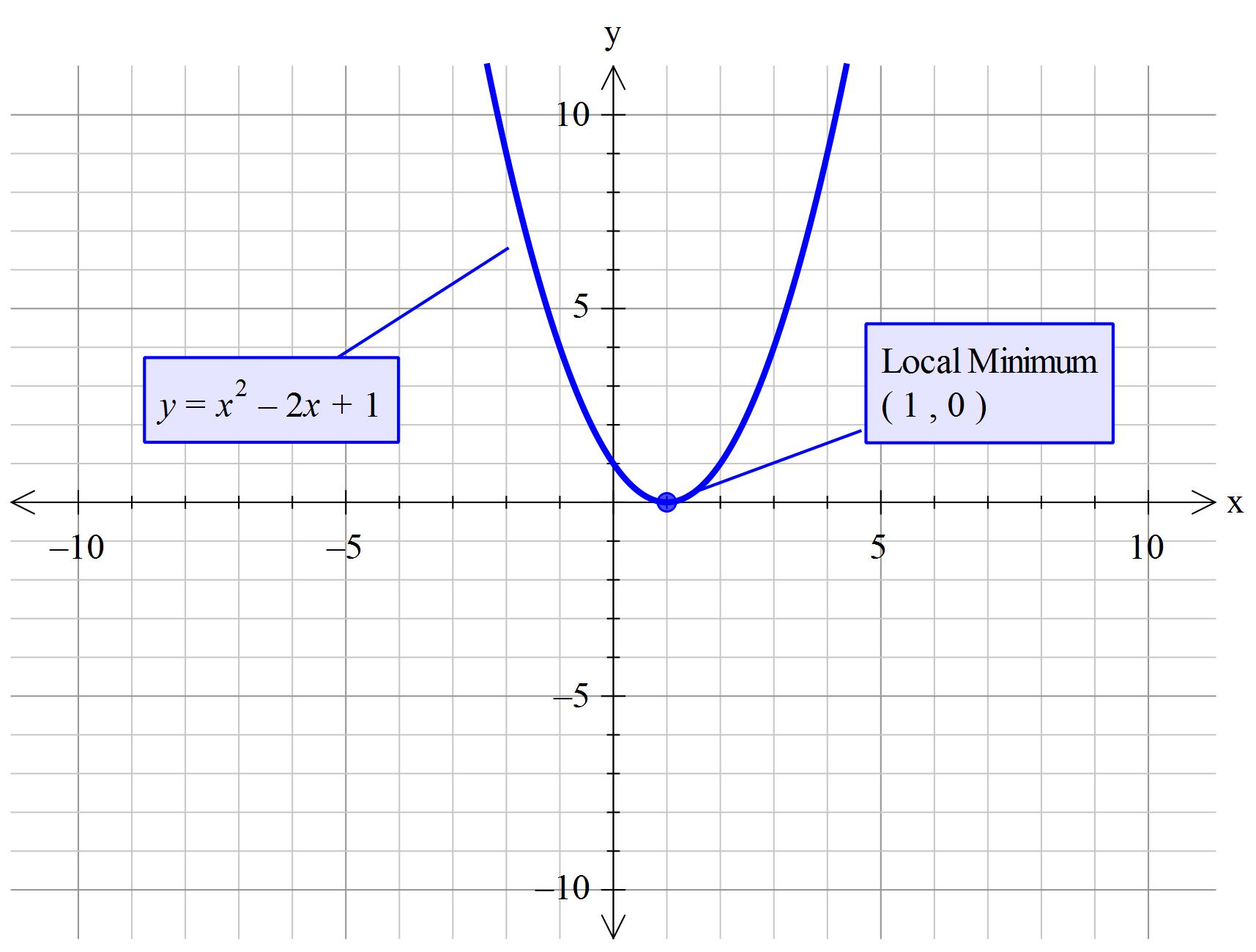



What Is The Vertex Of Y X 2 2x 1 Socratic
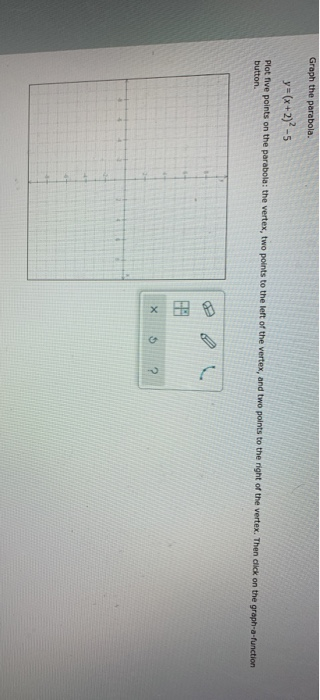



Graph The Parabola Y X 2 2 5 Plot Five Points On Chegg Com
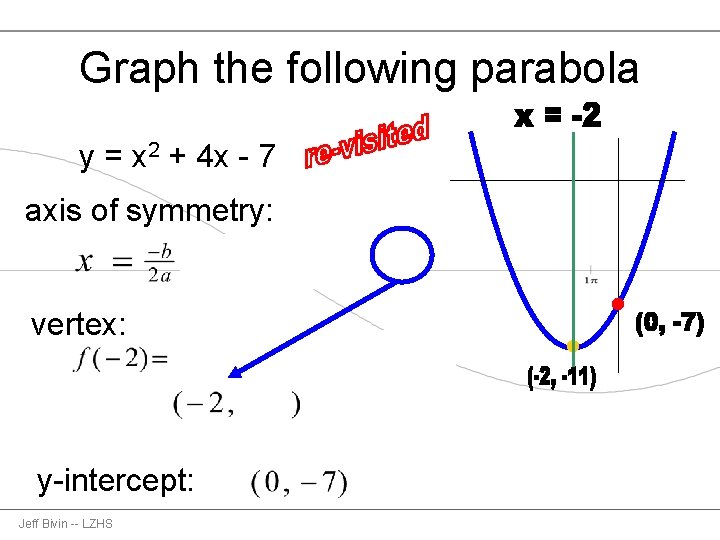



Graphing Parabolas Using The Vertex Axis Of Symmetry




Graphing Parabolas




Find The Area Of The Region Bounded By The Parabola Y X 2 And The Line Y 4 Study Com
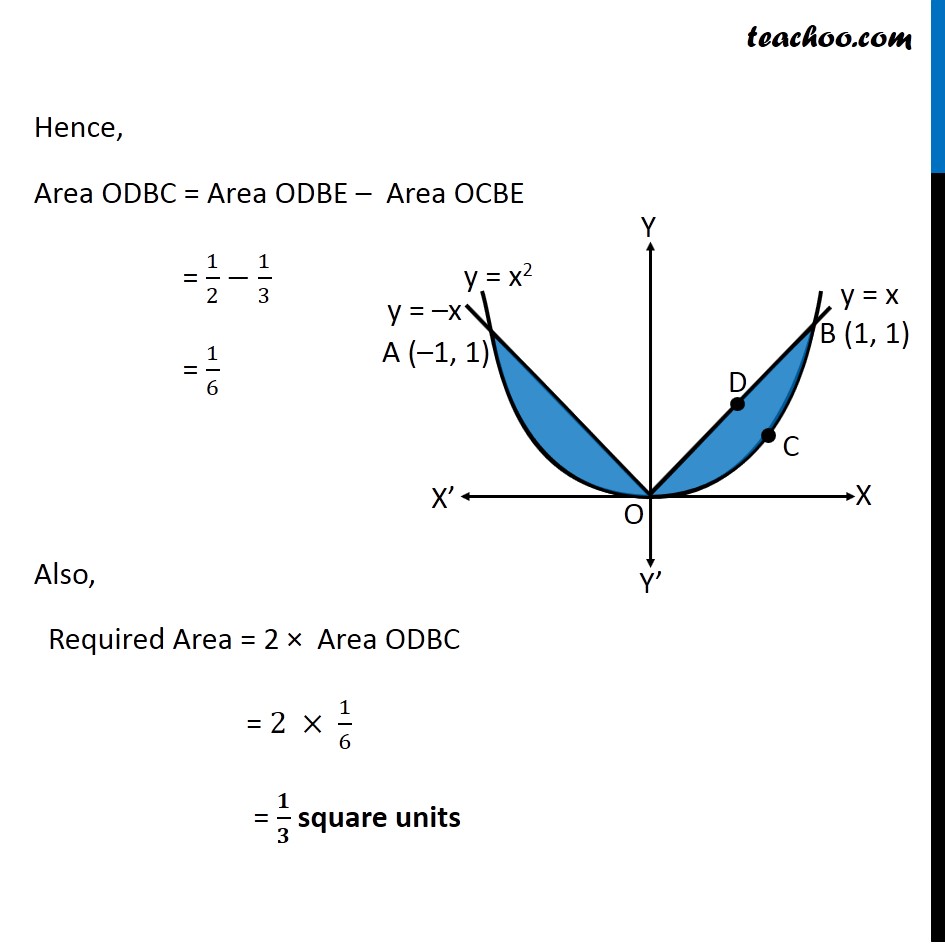



Misc 12 Find Area X Y Y X2 And Y X Class 12


